ODE Module
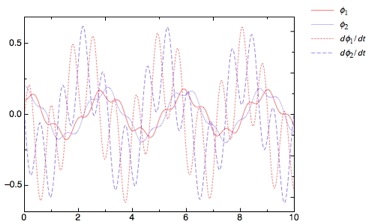
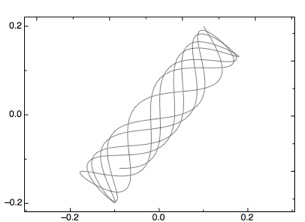
ODE Module ist ein pro Fit-Modul. Es löst Anfangswertprobleme mit gewöhnlichen Differentialgleichungssystemen erster Ordnung (bis zu 14 Gleichungen). Die Lösungen werden über die Integrationsvariable oder gegeneinander (Phasendiagramme) aufgetragen. Informationen über die wissenschaftliche Datenanalyseanwendung pro Fit findet man auf der QuantumSoft pro Fit Website. ODE Module ist Freeware.
Wie es funktioniert
Gewöhnliche Differentialgleichungen (englisch ordinary differential equations oder ODEs, daher der Name des Moduls) jeder Ordnung können auf einen Satz Differentialgleichungen erster Ordnung reduziert werden, den man numerisch integrieren kann. Die Differentialgleichungen können auch gekoppelt sein, d.h. es kann mehrere von der Zeit abhängige Variablen geben, die kombiniert vorkommen können. Betrachten wir eine einfache gewöhnliche Differentialgleichung zweiter Ordnung für die Funktion x(t) wie
x'' + q(t) x' = r(t) ,
wobei x' die erste und x'' die zweite Ableitung von x(t) nach t bezeichnet. Nun nennt man die erste Ableitung um
y = x'
und schreibt die Differentialgleichung so:
y' = r(t) - q(t) y .
Jetzt hat man einen Satz von zwei Differentialgleichungen erster Ordnung:
x' = y
y' = r(t) - q(t) y
Ausgehend von einem Startpunkt t0, an dem x und y (d.h. x') bekannt sind, kann man die Ableitungen von x und y berechnen und so zu einem zweiten Punkt t1 integrieren, wobei numerische Integrationsmethoden wie die Euler-Methode, Runge-Kutta oder ähnliche verwendet werden.
Eine Differentialgleichung dritter Ordnung resultiert demnach in einem Satz von drei Differentialgleichungen erster Ordnung, zwei Differentialgleichungen zweiter Ordnung resultieren in vier Differentialgleichungen erster Ordnung usw. Um für Systeme verschiedener Ordnungen flexibel zu bleiben, nutzen wir die folgenden Namenskonventionen in ODE Module:
y1 = x, y2 = y, y3 = z, ...
Dann schreiben wir die Differentialgleichungen von oben in der Form
y1' = y2
y2' = r(t) - q(t) y2
Zur Nutzung von ODE Module zur Integration von solchen Differentialgleichungssystemen muss man in pro Fit eine Funktion bereitstellen, die die Werte der Ableitungen an einem gegebenen Punkt über diesen Satz Differentialgleichungen berechnet. ODE Module nutzt die Runge-Kutta Methode (mit fester oder variabler Stützweite) zur Integration und ruft dazu diese Funktion auf. Weitere Informationen über die Installation und den Gebrauch von ODE Module findet man in der Readme-Datei.
Versionsüberblick
2.0
- Nutzung von VAR-Parametern für größere Geschwindigkeit und Stabilität (Bitte aktualisieren Sie Ihre "derivs"-Funktionen anhand der beigefügten Beispiele!)
- Version für pro Fit 7.0
- Version für pro Fit 6.1
- Mac OS X Universal (PPC und Intel)
- Vorgegebene Liniendicke 0.5 pt statt 0.25 pt
- Carbon-Version für pro Fit 5.6 bis 6.0
- Anzahl möglicher Gleichungen auf 14 erhöht
- Bugfix für N > 6 (Grenze der pro Fit InputBox-Funktion)
- Anzahl möglicher Gleichungen auf 12 erhöht
- Problem mit Phasendiagrammen bei konstanten Funktionen beseitigt
- Option zur Speicherung der Daten in einem pro Fit-Datenfenster hinzugefügt. Das ist nützlich zur weiteren Verarbeitung dieser Daten in pro Fit.
- Erstes öffentliches Release
Die Runge-Kutta-Algorithmen wurden von Press, Teukolsky, Vetterling, Flannery implementiert: Numerical Recipes in C, Cambridge University Press. pro Fit wird von QuantumSoft, Schweiz, hergestellt.
Garantie
Keine. ;-) Bitte melden Sie sich bei Problemen.